ブログ

2024.11.26 699 views

理論在庫（適正在庫）算定のかんどころ

• 全体サプライチェーン最適化
• 物流センター内改善

シニア・コンサルタント

安本　大地

プロフィール 関連トピックス

最近、業務上、理論在庫量を考察する機会を多く頂きましたので、今回は理論在庫について述べてみます。
今更ですが、当然ながら在庫管理は企業の運営において非常に重要な役割を果たします。適切な在庫管理はコストの削減と顧客満足度の向上につながります。本ブログでは、理論在庫の算定方法に焦点を当て、巷の教科書的な資料を補足する視点で、特に安全在庫を主体に語ってみます。

理論在庫とは

理論在庫とは、過去の出荷傾向や入荷の条件から理論的に求まる在庫量です。「適正在庫」と言うこともありますが、個人的には「適正」という言葉には違和感を持っており、「適正」かどうかは別問題だと思っています。
確かに、そのときの制約下では「適正」なのかもしれませんが、発注単位や入荷頻度が変更されれば変わる値ですので、「適正」というよりは、あくまで、その時点での条件から理論的に求まる「理論」上の在庫に過ぎないと考えています。
もちろん、現時点で「理論」在庫よりも多くの在庫を抱えてしまっているときは、在庫削減を検討すべきです。そういった目安にはなります。しかし逆に、現状が「理論」在庫程度になっていたとしても、それは今の状態が「適正」であるという意味ではなく、リードタイムや発注単位等の条件を変更することができれば、もっと良い状態になる可能性があります。そのような場合は、その変更の可能性を探り、もっと良い状態に近づけていくべきもので、そうすることで「適正」に近づくのだろう、というのが私の考えです。

理論在庫の算定方法

理論在庫は、２段構造になっています。安全在庫とサイクル在庫から構成されます。

理論在庫＝安全在庫＋サイクル在庫

安全在庫とは

安全在庫は、予測外の需要の増加やリードタイムの遅延に対処するための余裕部分です。想定外の事態が起きても欠品を起こさないために、通常想定される出荷を満たす分より余分に在庫として持っておく分のことを言います。

安全在庫の量は、需要の変動や納品リードタイムに基づいて決定されます。一般的には、次の式を用います。

安全在庫＝ｋ×σ×√LT

ここに、
ｋ：安全係数
σ：出荷量の標準偏差
LT：納品リードタイム

これはどういう意味かというと、
一般に日々の需要量（＝倉庫からの出荷量）は変動します。平均的な需要量に対し、日々どのくらいずれる可能性があるかを考えます。多めにずれ続け、それが一定期間続いたときに、最終的に（次の入荷までに）どのくらいのずれになる可能性があるか、ということで、その大きさが安全在庫量となります。

「日々どのくらいずれる可能性があるか」が標準偏差（σ）です。一般的に日別の出荷量データの標準偏差を求めます。標準偏差の単位は算出の基の出荷量の単位と同じになります。個なら個ですし、ケースならケース、パレットならパレットです。（ここでは「個」で話を進めます）
「一定期間続いたとき」の期間の要素を織り込むために、期間の平方根をとるのが分かりにくいところですが、これは一般的に「分散の加法性」ということで説明されます。日々のずれる可能性を日数分積み上げるには、数学的には分散を使うということです。

分散（σ²）は標準偏差（σ）の２乗です。これを日数分積み上げます。すなわち、期間（LT）分の分散は、

σ²×LT

で表されます。これの平方根をとると、標準偏差×√期間　となります。これがLT期間分の標準偏差の大きさということになります。

σ×√LT

なお、LTの単位は、標準偏差を算出している単位期間に合わせます。日データで標準偏差を算出しているなら、LTの単位も（日）にします。

安全係数（ｋ）についてですが、この理論はあくまで確率統計的に処理をして組みあがっている理論なので、理論上、小さい確率ではものすごくずれることもある、ということになります。ですので、許容欠品率と安全係数という考え方を入れて、ずれの上限を決めることをします。許容欠品率に応じて数学的に決まっている安全係数という係数をσに掛けます。

下はネットから拾ってきた標準偏差の説明です。

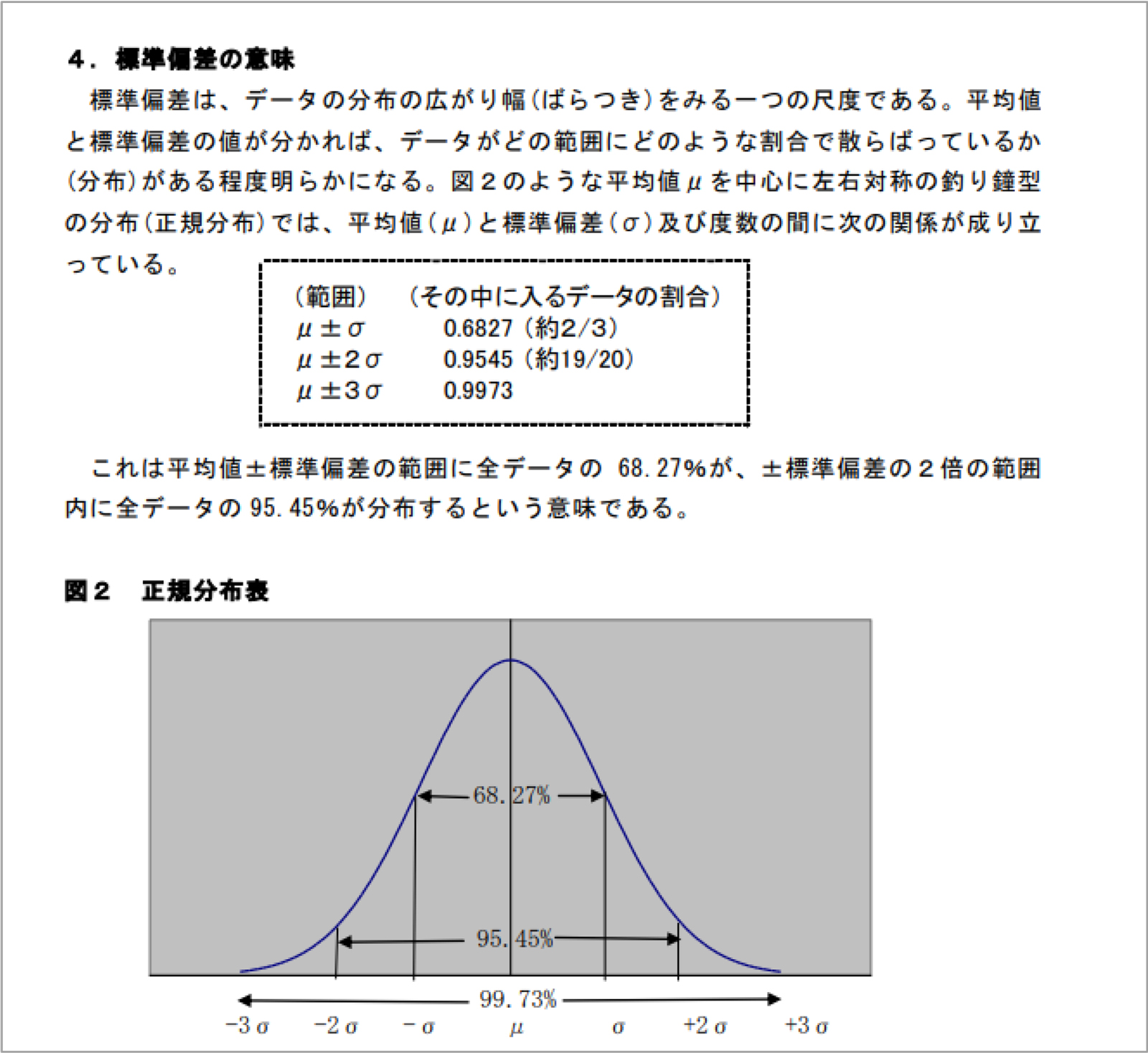
出所：富山県ＨＰ「統計指標のかんどころ」

この上の資料で言うところの「μ±2σ」や「μ±3σ」の「2」や「3」が安全係数に相当するものです。
そして、上の資料で言うところの、例えば「μ±2σ」のときの「95.45％」の外側分、すなわち100％との差、100－95.45＝4.55％の、さらに片側分、4.55÷2＝2.275％　が許容欠品率に相当するものとなります。（足りなくなる側だけ見るので片側分だけ見ます。予想に反して出荷が少なく在庫が余っている、という事象はここでは関心事でありません。）
なお、この「95.45％」の数字を信頼区間と言います。安全在庫の検討では、許容欠品率5％で見ることが多いですが、そのときの信頼区間は90％となるわけです。（両側に5％ずつあるので）
そして、信頼区間90％のとき、「95.45％」のとき「2」だった値は1.65（これは数学的に決まっている値）となります。この「1.65」という値を安全在庫の議論では安全係数（ｋ）と呼んでいるのです。
図に書き込むとこのような感じです。

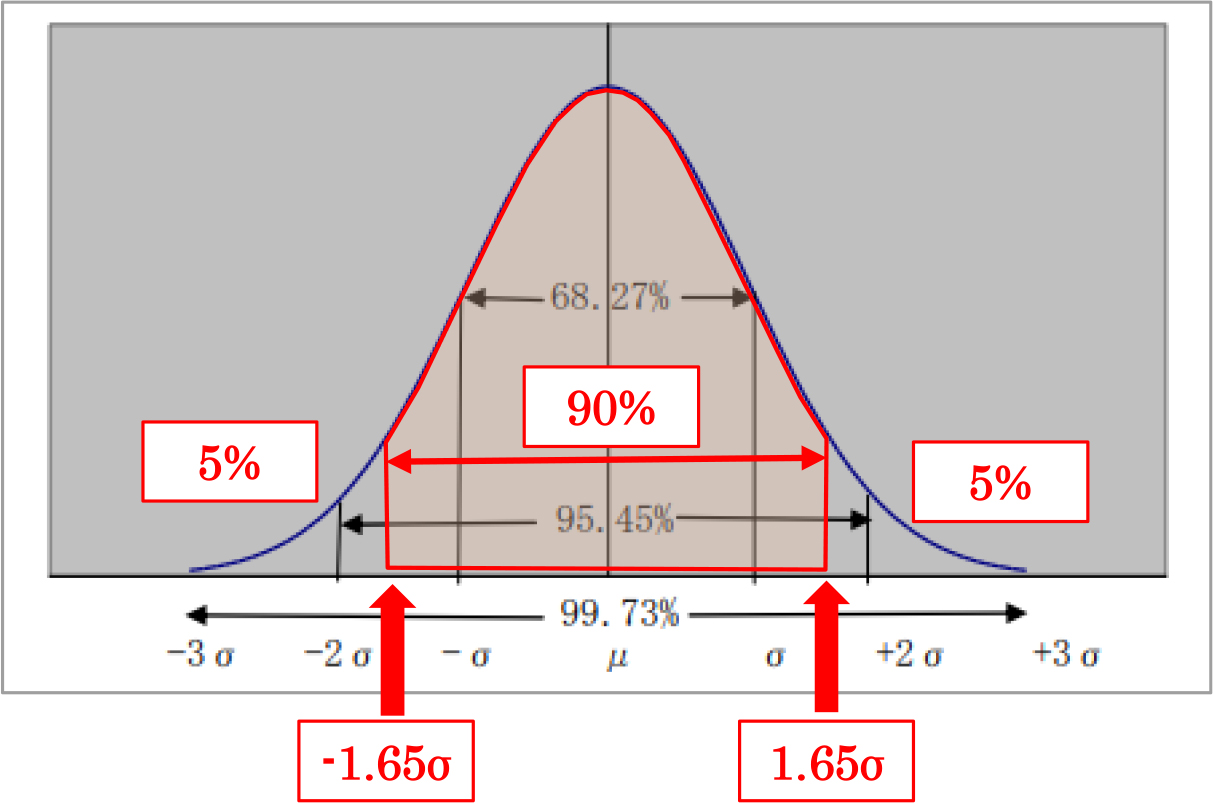
出所：富山県ＨＰ「統計指標のかんどころ」の図にNX総研が加筆

許容欠品率5％とは、正規分布の端の部分の「5％の確率で起こり得る、予想に反してたくさん出荷がかかって在庫が足りなくなる」という事象に関しては諦めて欠品として許容する、という意味です。
ちなみに、許容欠品率3.0%（信頼区間94％）のときは安全係数1.89、許容欠品率2.5％（信頼区間95％）のときは安全係数1.96となります。（繰り返しですがこれは数学的に決まっている値です）

ということで、所定の許容欠品率の分散は　k×σ（個）となります。これのLT期間分ということで√LTを掛けて、

安全在庫＝ｋ×σ×√LT

となるのです。

なお、この論理は、安全在庫部分について統計的に処理していることから、出荷量の値の散らばり具合がある程度正規分布に乗る、ということが条件になります。
また、一定の割合の欠品を許すことも条件になります。絶対に欠品を許さない、欠品率0％という条件だと、この理論ではその際の安全在庫量は無限大になってしまうのです。
ですので、出荷の値の散らばり具合が正規分布として捉えられない場合や、欠品が許されない条件下では、適応しにくい理論となります。

サイクル在庫とは

サイクル在庫は、通常の需要を満たすために定期的に発注され、入荷され、保管される在庫です。基本的に入荷と入荷の間に出荷される量となります。入荷から次の入荷までの間に滞留して在庫として保管している分という意味です。入荷のときに一度在庫が増えて、需要に応じて少しずつ出荷することで在庫が減っていき、次の入荷でまた一気に増えます。ですので変動しますが、考え方としてはこの平均の量をとります。一般に、

サイクル在庫＝発注量の1/2

とします。「発注量分が一気に入荷して、少しずつ出荷され、次の入荷時には前の入荷量分はすべて出きった」としてその期間の平均を取っている、ということです。

このとき、発注量は発注単位の整数倍になるので、発注単位が小さいほど、最小限の発注量で済むということになります。例えば、350欲しいときに、発注単位が10なら350注文できますが、発注単位が100なら400注文することになります。さらに1000であれば1000注文するしかありません。
ですので、発注単位は小さい方がサイクル在庫を小さくすることができ、結果、理論在庫も小さくなります。

在庫維持月数（日数）・回転率

在庫維持月数（日数）と回転率についても述べておきます。
平均在庫量を出荷量で割ったものが在庫維持月数（日数）です。平均在庫量が500個で出荷量が1000個/月であれば、

在庫維持月数＝500÷1000＝0.5（ヶ月）

です。「その在庫量で出荷量に対して半月持ちこたえる（維持できる）」という意味になります。
回転率は、この逆数です。

回転率＝1000÷500＝2（回転）

「ひと月に在庫が２回入れ替わる」という意味になります。

まとめ

在庫管理は、企業の資産効率と顧客満足度に直結する重要な要素です。理論在庫の算定方法を理解し、安全在庫とサイクル在庫を適切に管理することで、在庫の過不足を防ぎ、運営の安定性を高めることができます。
巷の解説資料でも計算式自体はたくさん記載があるので計算するだけなら事足ります。ですが、計算の捉え方の記述が不足しているものが多いと思いましたので、本稿ではそれを補足するつもりで書いてみました。

（この記事は2024年11月19日時点の状況をもとに書かれました。）